Teori
Peluang
Hampir
semua kejadian di dunia ini sifatnya tidak pasti. Terlebih lagi kalau kejadian tersebut
menyangkut masa yang akan datang. Dari tebakan itu muncul kemungkinan atau
peluang atau probabilitas kejadian yangbersangkutan yang kemudian melahirkan
sebuah teori yang dikenal sebagai teori
probabilitas.
Saat ini teori peluang
telah menjadi suatu alat penting dalam berbagai bidang rekayasa, meteorologi,
asuransi,operasi-operasi bisnis, dan berbagai bidang eksperimen. Bahkan teori
peluang menjadi dasar metode statistik, yaitu suatu bidang matematika yang
aplikasinya hampir meliputi semua bidang.
Konsep-konsep probabilitas
didukung oleh banyak teori, seperti teori himpunan, permutasi, dan kombinasi.
A. Himpunan
- Pengertian Himpunan
Himpunan adalah
kumpulan objek yang didefinisikan dengan jelas dan dapat dibeda-bedakan. Setiap
objek yang secara kolektif membentuk himpunan tersebut disebut elemen atau
unsur atau anggota dari himpunan tersebut.
Himpunan
dilambangkan dengan sepasang kurung kerawal {} dan biasanya dinyatakan
dengan huruf besar, seperti A, B, C, ….Anggota himpunan dinyatakan dengan Î dan bukan himpunan
dilambangkan dengan Ï. Dalam statistk himpunan
dikenal sebagai populasi.
- Penulisan
Himpunan
Himpunan
dapat ditulis dalam dua cara, yaitu cara pendaftaran dan cara pencirian.
a. Cara pendaftaran
Dengan
cara pendaftaran, unsur himpunan ditulis satu persatu atau didaftar
Contoh
:
1) A =
{a,i,u,e,o}
2) B =
{1,2,3,4,5}
b. Cara pencirian
Dengan cara pencirian,
unsur-unsur himpunan ditulis dengan menyebutkan sifat-sifat atau ciri-ciri
unsur himpunan tersebut.
Contoh :
1)
A
= {X : x huruf hidup}
2)
B
= {X : 1 £ x £ 5 }
Tanda
(:) dibaca sedemikian rupa, sehingga atau X dimana
- Macam-macam himpunan
a. Himpunan
semesta
Himpunan
semesta adalah himpunan yang memuat seluruh objek yang dibicarakan atau
himpunan yang menjadi objek pembicaraan. Himpunan semesta dilambangkan dengan S
atau U
Contoh :
S = U = {a, b, c, ......}
S = U = {X : x bilangan
asli }
b.
Himpunan
Kosong
adalah himpunan yang tidak
memiliki anggota. Himpunan kosong dilambangkan dengan f atau { }
c.
Himpunan
bagian
Adalah
himpunan yang menjadi bagian dari himpunan lain. Himpunan bagian dilambangkan Ì, Banyaknya himpunan bagian
dari sebuah himpunan dengan n unsur adalah 2n.
Contoh :
Jika
diketahui A = {1,2,3}, tentukan banyaknya himpunan bagian dari A dan tuliskan
himpunan-himpunan bagian tersebut.
Penyelesaian
:
-
Banyaknya
himpuan bagian A adalah 23 = 8
-
Himpunan
bagian di atas adalah : { }, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}
d.
Himpunan
komplemen
Adalah
himpuan semua unsur yang tidak temasuk dalam himpunan yang diberikan. Jika
himpunannya adalah A maka himpunan komplemennya dilambangkan Ac atau
A’ atau A rata-rata.
Contoh :
Jika
diketahui S = {1,2,3,4,5,6,7}
B = {2,3,4}
Penyelesaian
:
Bc
= {1,5,6,7}
Diagram
Vennya adalah :
Bc = daerah yang
diarsir
Digram Venn Himpunan Bc
- Operasi Himpunan
a. Operasi
gabungan (union)
Gabungan dari himpunan A dan himpunan B adalah semua
unsur yang termasuk di dalam A atau didalam B atau di dalam A dan B sekaligus.
Gabungan dari himpunan A dan himpunan B dilambangkan A È B
atau A + B. Dituliskan : A È B
= {X : x Î A, x Î B,
atau x Î AB}.
Diagram Vennnya :
A È B daerah yang diarsir
Contoh
soal:
Jika diketahui:
S = {
X : 0 < x < 10}
P = {2,3,5,7}
G = {2, 4, 6, 8, 10}
Tentukan: P È G!
Penyelesaian :
P È G = {2, 3, 4, 5, 6, 7, 8, 10}
b.
Operasi irisan (interseksi)
Irisan dari himpunan A dan B adalah himpunan semua unsur yang termasuk di dalam A dan di dalam B. Irisan dari himpunan A dan himpunan B dilambangkan A Ç B atau AB dan dituliskan:
A Ç B = {X :
x Î A dan x Î B}.
Diagram
Vennya :
Diagram venn
dari A Ç B
Contoh soal:
Jika diketahui: S = {X : 2 £ x £ 8}
P = {2, 3, 5, 7}
A = {2, 3, 4, 6} Tentukan PÇ A !
Penyelesaian: P Ç A = {2, 3}
c. Operasi selisih
Selisih himpunan A dan B adalah himpunan semua unsur A yang tidak termasuk di dalam B. Selisih himpunan A dan himpunan B dilambangkan A - B atau AÇ Bc. Dituliskan: {X : x Î A dan x Ï B) atau {X : x Î A dan x Î Bc}.
Diagram Vennnya:
Diagram Venn dari A – B
Contoh
soal: Jika
diketahui: S = {1, 2, 3, 4, 5, 6, 7, 8, 9}
P
= {2, 3, 5, 7}
G
= {2, 4, 6, 8}
Tentukan
P – G !
Penyelesaian:
P-G={3, 5, 7}
5.
Berapa Aturan dalam Himpunan
Contoh soal:
Suatu kelas yang jumlah mahasiswanya 70 orang, 50
orang di antaranya senang statistik, 40 orang senang matematika, serta 30 orang
senang statistik dan matematika.
a. Berapa orang yang tidak senang statistik dan
matematika?
b. Gambarkan diagram Vennnya!
Penyelesaian
:
a. n(S) = 70 orang, n(St) = 50 orang, n(M) = 40 orang, n(St Ç M) = 30 orang.
n(St È M) = n(St) + n(M) - n(St Ç M) = 50 + 40 - 30 = 60 orang
n(St Ç M)c = n(S) - n(St
È M) = 70-60 = 10 orang
b.
Diagram Vennnya:
Diagram Venn dari n(St Ç M)c
B. Permutasi dan Kombinasi
1. Prinsip dasar membilang
Jika kejadian pertama dapat terjadi dalam n1 cara, kejadian kedua dalam n2. cara, demikian seterusnya, sampai kejadian k dalam nk cara, keseluruhan kejadian dapat terjadi dalam:
n1 x n2 x ... x nk, cara
Contoh soal:
Seorang pengusaha ingin bepergian dari Jakarta ke
Ujungpandang melalui Surabaya. Jika Jakarta-Surabaya dapat dilalui dengan tiga
cara dan Surabaya-Ujungpandang dapat dilalui dengan dua cara, ada berapa cara pengusaha
tersebut dapat tiba di Ujungpandang melalui Surabaya?
Penyelesaian:
Misalkan: dari Jakarta ke Surabaya
(n1) = 3 cara
dari Surabaya ke Ujungpandang (n2) = 2 cara
Cara pengusaha tersebut dapat
tiba di Ujungpandang melalui Surabaya
adalah:
n1 x n2 = 3x2 = 6 cara
2.
Faktorial
Faktorial adalah perkalian semua bilangan bulat
positif (bilangan asli) terurut mulai dari bilangan 1 sampai dengan bilangan
bersangkutan atau sebaliknya. Faktorial dilambangkan: "!".
Jika: n = 1, 2, maka:
n! = n(n - 1) (n - 2) ... x 2 x 1
= n(n
- 1)!
Catatan:
1! = 1
0! = 1
Contoh soal:
Tentukan nilai faktorial dari bilangan berikut!
a. 5!
b. 3! x 2!
c.
a. 5! = 5x4x3x2xl
= 120
b. 3! x 2! = 3 x 2 x 1 x 2 x 1 = 12
c.
a. Pengertian permutasi
Permutasi adalah suatu penyusunan atau pengaturan beberapa objek ke dalam
suatu urutan tertentu.
Contoh:
1)
Ada 3 objek, yaitu ABC. Pengaturan objek-objek tersebut ialah ABC, ACB, BCA, BAC, CAB, CBA yang disebut permutasi. Jadi, permutasi 3 objek menghasilkan enam
pengaturan dengan cara yang berbeda.
2)
Pengaturan 4 huruf dari 6 huruf
pertama dalam abjad menghasilkan 360 cara yang berbeda.
Posisi 1
|
Posisi 2
|
Posisi 3
|
Posisi 4
|
tersedia
|
tersedia
|
tersedia
|
tersedia
|
pilihan
|
pilihan
|
pilihan
|
pilihan
|
6x5x4x3
|
|||
Dari contoh tersebut, dapat diketahui bahwa
banyaknya permutasi yang mungkin bergantung pada:
1) ukuran kelompok asalnya,
2) banyaknya objek yang dipilih dari kelompok itu.
b. Rumus-rumus permutasi
1) Permutasi dari n objek tanpa
pengembalian
a) Permutasi dari n objek seluruhnya
Permutasi dari n objek seluruhnya tanpa pengembalian dirumuskan;
nPn = n!
Contoh soal:
(1) Tentukan
nilai dari 4P4!
Penyelesaian'.
Penyelesaian'.
4P4 = 4! = 4 x 3 x 2 x 1 = 24
(2) Pada suatu tempat terdapat 4 buku matematika yang berbeda,
3 buku statistik yang berbeda, dan 2 buku akuntansi. Semua
buku akan disusun pada sebuah rak buku. Berapa cara susunan
yang mungkin dari kejadian berikut ini?
3 buku statistik yang berbeda, dan 2 buku akuntansi. Semua
buku akan disusun pada sebuah rak buku. Berapa cara susunan
yang mungkin dari kejadian berikut ini?
(a) • Buku-buku matematika dapat disusun.
•
Buku-buku statistik dapat
disusun.
•
Buku-buku akuntansi dapat
disusun.
•
Ketiga kelompok buku itu dapat
disusun.
(b) Masing-masing kelompok buku (subjek)
disusun bersama
(dijadikan satu).
(dijadikan satu).
Penyelesaian:
(a) • Buku-buku matematika
dapat disusun dalam:
4P4 = 4! =
4 x 3 x 2 x 1 = 24 cara
• Buku-buku statistik dapat disusun dalam:
3P3 = 3! = 3 x 2 x 1 = 6 cara
• Buku-buku akuntansi dapat
disusun dalam:
2P2 = 2! = 2 x 1 = 2 cara
• Ketiga kelompok buku dapat
disusun dalam:
3P3 = 3! = 3 x 2 x 1 = 6 cara
(b) Masing-masing kelompok buku disusun
bersama dalam:
4! x
3! x 2! x 3! = 24 x 6 x 2 x 6 = 1.728 cara
b) Permutasi sebanyak r dari n objek
Permutasi sebanyak r dari n objek tanpa pengembalian dirumuskan:
Contoh Soal :
(1) Tentukan nilai dari 6P4!
Penyelesaian :
(2) Dari empat calon pimpinan
sebuah perusahaan, misalkan A, B, C, dan D hendak dipilih seorang ketua, seorang sekretaris, dan seorang bendahara.
(a)
Berapa cara keempat calon
tersebut dipilih?
(b)
Tuliskan kemungkinan susunannya!
Penyelesaian :
n = 4 dan r = 3
b. Kemungkinan susunannya
ABC, ABD, ACB, ADB, ADC, ACD BAC, BAD, BCA, BCD, BDA, BDC CABy
CAD, CBAf CBD, CDA, CDB
DAB, DAC, DBA, DBC, DCA, DCB
b Permutasi sebanyak r dari n objek
Permutasi sebanyak r dari n objek tanpa pengembalian dirumuskan:
Contoh soal
(1) Tentukan nilai dari 6P4
(2) Dari empat calon pimpinan sebuah perusahaan, misalkan A, B, C, dan D hendak dipilih seorang ketua,
seorang sekretaris, dan seorang bendahara.
(a) Berapa cara keempat calon
tersebut dipilih?
(b) Tuliskan kemungkinan susunannya!
Penyelesaian: n = 4 dan r = 3
(b) Kemungkinan susunannya adalah
ABC, ABD, ACB, ADB, ADC, ACD BAC, BAD, BCA, BCD,
BDA, BDC CAB, CAD, CBA,
CBD, CDA, CDB DAB, DAC, DBA, DBC, DCA, DCB






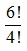







Tidak ada komentar:
Posting Komentar